Unit 1 Mechanics and the properties of Matter
1.1 Vectors
Learning Outcomes
- Distinguish between distance and displacement.
- Distinguish between speed and velocity.
- Define and classify vector and scalar quantities.
- Use scale diagrams, or otherwise, to find the magnitude. and direction of the resultant of a number of displacements or velocities.
- State what is meant by the resultant of a number of forces.
- Carry out calculations to find the rectangular components of a vector.
- Use scale diagrams, or otherwise, to find the magnitude and direction of the resultant of a number of forces.
Aids to Understanding
Distance and Displacement
Where did the (230)come from and why do we need it? Estimate the distance you might walk on a typical school day and compare it with your overall displacement.
Speed and Velocity
Look at the diagram of the Moon and Earth. Suppose the moon is above the Earth as shown. Suppose this position is UP. After 15 days the Moon will be below the Earth and suppose this position is DOWN. Calculate the velocity, average speed, distance travelled and displacement of the moon during this 15 day period. Information you may need is readilly available on the internet.
Scalars and Vectors
Impulse is defined as Force x Time and is a vector. However Work done is defined as Force x Displacement and is a scalar. The rule is a vector x vector = scalar but vector x (or divided by) scalar = vector. This also follows from the vector dot product a.b you may have studied in maths. If Pressure = Force/Area, is pressure a vector or Scalar?
Scale Diagrams
Try the following problem. Remember the resultant vector is always drawn at the centre of the compass. Suppose our ship now travels with a bearing 080o for 6km, the ship changes direction and travels with a bearing 200o for 4 km, the ship again changes direction and travels a further 10 km on a bearing of 140o. Find the the resultant displacement vector, ie locate the position of the ship relative to where it started.
Resultant Force
Suppose a 2 kg picture is hanging on the wall. It is not moving so the upwards force due to the two strings is equal to
the weight of the picture. Using a scale diagram, or otherwise, find the force exerted by each string. The force exerted by
a string (or rope or cable) is called the Tension in the string.

Rectangular components of a vector
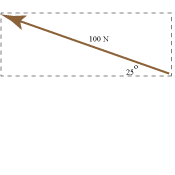
Suppose a person pulls a 50 kg lawn mower with a force of 100 N at an angle of 25o.
Find the horizontal and vertical components
of the force. NOTE: The person is exering an upwards force and a horizontal force on the lawn mower but it
only moves horizontally and not upwards. Why is this?
1) Distance and Displacement
Suppose a dog walks round a rectangle from A to B. The total distance travelled by the dog is 17 m, however the displacement of the dog is the direct distance from where the dog started to where he ended. Thus the displacement of the dog is 13m (230) (ie 13m relative to where the dog started). Also, the moon travels a great distance round the Earth each month but its displacement is zero. Note: We speak of distance travelled by a body and the displacement of a body. This is the difference between distance and displacement.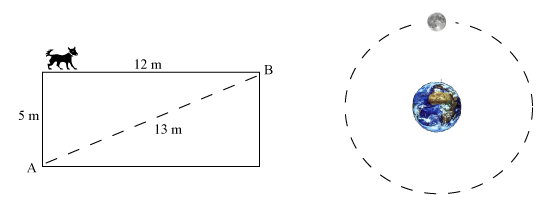
2) Speed and Velocity
The speed of a body is simply the distance the body covers in unit time (second, minute, hour). However, the average velocity of a body indicates the distance covered in a unit time in a given direction.
To help distinguish speed and velocity further consider the following. If a car had an average speed of 20 ms-1 for a one hour journey, it is unlikely the car travelled at a constant speed of 20ms-1 for the full hour, indeed it may have travelled at that speed for only brief instances. A similar argument holds with the direction part of an average velocity. Although our plane had travelled in a Northerly direction and its final velocity is given as North, at only one point (extreme West) was it travelling due North. In fact over the 200 s we say the plane covered 0.1 km every second in a Northerly direction. (even if it only headed due North only once and never at 0.1 kms-1. You should be able to see how these concepts are useful for navigators in ships and aeroplanes. The velocity and speed of a body will have the same magnitude only if the motion is in one dimension and the body does not reverse its direction. Even though the Earth travels round the Sun at a great speed, its average velocity is zero.
You are invited to calculate the speed and velocity of the plane after 300 s, if it continues in the same circular route.
3) Scalars and Vectors
Scalars are physical quantities that have magnitude (size) only and thus can be defined by one number (with unit). For example the speed of the aeroplane was 0.16 m-1 and thus this single value completely defined the physical quantity we call speed. Speed is a Scalar. Vectors are physical quantities that have magnitude and direction and thus require two values to completely describe them. For example the velocity of our plane was 0.1 ms-1, North. and thus two values are required to define the physical quantity we call velocity. The angle provides information about direction. Velocity is a vector. The table below lists some of the scalars and vectors we work with in this course.| Scalar | Vector |
|---|---|
| Distance | Displacement |
| Speed | Velocity |
| Mass | Weight (force) |
| Time | Acceleration |
| Temperature | Impulse |
4) Scale diagrams and Resultants
Vectors are represented by arrows. The magnitude of the arrow is its magnitude and the arrow indicates its direction The resultant vector is the sum of two or more vectors. If the vectors span two (or more) dimensions then direct addition is
not possible and an accurate scale drawn must be drawn. The following example illustrates this.
Example: It is a calm day at sea and a ship is sailing through the water. The ship travels with a bearing 060o
for 10km, the ship changes direction and travels with a bearing 110o for 5 km, the ship again changes
direction and travels a further 8km on a bearing of 300o. Find the the resultant displacement vector,
ie locate the position of the ship relative to where it started.
The resultant vector is the sum of two or more vectors. If the vectors span two (or more) dimensions then direct addition is
not possible and an accurate scale drawn must be drawn. The following example illustrates this.
Example: It is a calm day at sea and a ship is sailing through the water. The ship travels with a bearing 060o
for 10km, the ship changes direction and travels with a bearing 110o for 5 km, the ship again changes
direction and travels a further 8km on a bearing of 300o. Find the the resultant displacement vector,
ie locate the position of the ship relative to where it started.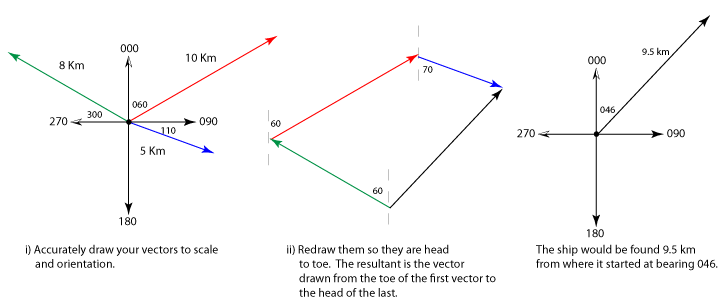
5) Resultant Force
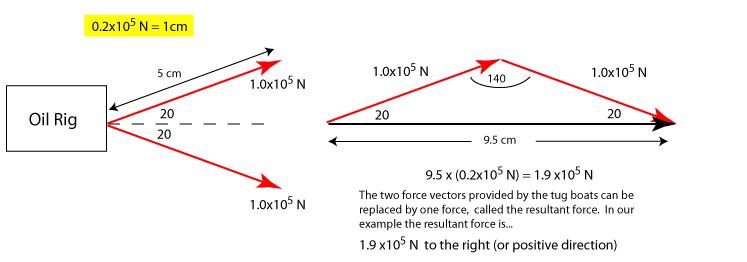
The resultant force vector is calculated in the same way as the resultant displacement vector, but they are thought of differently. Where the resultant displacement vector locates the position of a body relative to where it started, the resultant force vector is the single force that is equivalent to the two or more force vectors that made it up. The following example illustrates this.Ex: Two tug boats are pulling an oil platform out to sea. The boats each exert a force of 1.0x105 N at an angle of 20o as shown. Find the resultant force vector, ie find the single force vector that is equivalent to the two vectors that made it up.
6) Rectangular Components of a Vector
The resultant vector is generally the sum of many vectors. When presented with a vector it is often useful to calculate its rectangular components. These rectangular components can be represented as vectors and their magnitude can be measured directly or calculated using simple trigometry. To find the direction of these vectors we use the head to toe method of vector addition The vector below represents a velocity vector and its rectangular components are called i) Horizontal component of velocity (ie in our example this is; 43.3 ms-1) ii) Vertical component of velocity (ie in our example this is; 25.0 ms-1)
Click for vector homework suggestion :) Click for solutions